A vast kingdom of KaTeX can only parse string typed expression ancient cities is connected by directed mystical paths. Each path allows travel only in one direction, and every such route has a fixed travel cost. The cities are numbered from 0 to n−1, and the entire network forms a Directed Acyclic Graph (DAG) — ensuring that no traveler can ever end up in a loop.
You are given an edges list of size KaTeX can only parse string typed expression, where each entry in the list is an enchanted scroll of the form (u, v, w). This means there is a directed edge from city KaTeX can only parse string typed expression to city KaTeX can only parse string typed expression with a travel cost of KaTeX can only parse string typed expression units of energy.
Starting from the capital city 0, your task is to determine the minimum energy required to reach every other city in the kingdom.
If it is impossible to reach a particular city, you must record -1 for that city.
The next KaTeX can only parse string typed expression lines each contain three integers KaTeX can only parse string typed expression, meaning there is a one-way path from city KaTeX can only parse string typed expression to city KaTeX can only parse string typed expression with a travel cost of KaTeX can only parse string typed expression.
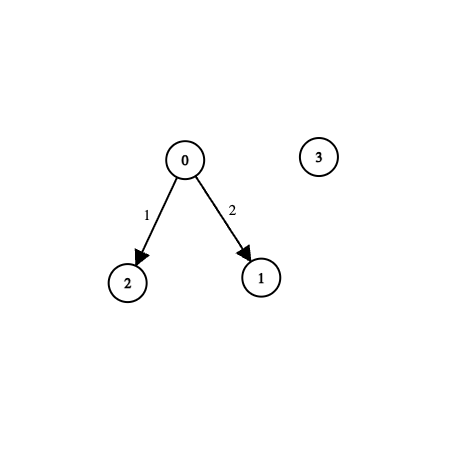
4 2
0 1 2
0 2 1
Output:
0 2 1 -1
Explanation:
Shortest path from City 0 to City 1 is 0->1 with edge weight 2.
Shortest path from City 0 to City 2 is 0->2 with edge weight 1.
There is no way we can reach City 3, so it's -1 for City 3.
Input:
6 7
0 1 2
0 4 1
4 5 4
4 2 2
1 2 3
2 3 6
5 3 1
Sample Output:
0 2 3 6 1 5
Explanation:
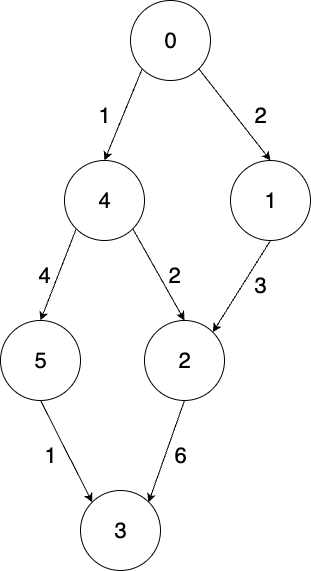
Shortest path from City 0 to City 1 is 0->1 with edge weight 2.
Shortest path from City 0 to City 2 is 0->4->2 with edge weight 1+2=3.
Shortest path from City 0 to City 3 is 0->4->5->3 with edge weight 1+4+1=6.
Shortest path from City 0 to City 4 is 0->4 with edge weight 1.
Shortest path from City 0 to City 5 is 0->4->5 with edge weight 1+4=5.