Question
Shortest Path of Safe Tiles
You are exploring a magical land grid of size n x n made of square tiles.
Each tile is either:
-
0 → a safe tile you can walk on
-
1 → a blocked tile you cannot step on
You start at the top-left corner of the grid (0, 0) and want to reach the bottom-right corner (n−1, n−1).
You can move in 8 directions—up, down, left, right, or diagonally—just like moving to any of the surrounding tiles.
Find the shortest number of tiles you must step on to reach the destination only through safe tiles (0).
If you cannot reach the destination at all, return -1.
Input
The first line contains a integer n denoting the size of the grid.
The following n line contains n space-separated values of the grid.
The following n line contains n space-separated values of the grid.
Output
Print the shortest number of tiles you must step on to reach the destination. If you cannot reach the destination at all, print -1.
Example
Input 1
2
0 1
1 0
Output 1
2
Explanation
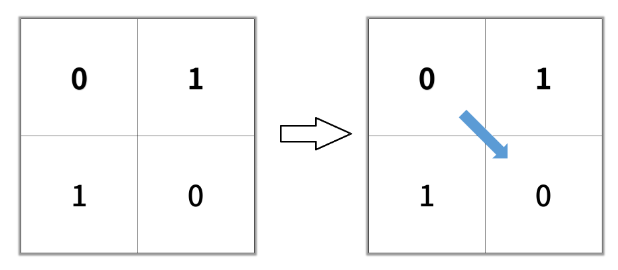
In the given 2×2 grid, we start at cell (0, 0) and want to reach cell (1, 1). Since both these cells contain 0 and diagonal movement is allowed, we can move directly from (0, 0) to (1, 1) in one diagonal step. As the path includes two cells, the length of the shortest path is 2.
Input 2
3
1 0 0
1 1 0
1 1 0
Output 2
-1
Explanation
In this 3×3 grid, the starting cell (0, 0) contains a 1, which means it is blocked and cannot be used to begin the path. Since the path must start at (0, 0) and only move through cells with value 0, there is no valid path to reach the bottom-right cell (2, 2). Therefore, the output is -1, indicating that no path exists.
2
0 1
1 0
Output 1
2
Explanation

In the given 2×2 grid, we start at cell (0, 0) and want to reach cell (1, 1). Since both these cells contain 0 and diagonal movement is allowed, we can move directly from (0, 0) to (1, 1) in one diagonal step. As the path includes two cells, the length of the shortest path is 2.
Input 2
3
1 0 0
1 1 0
1 1 0
Output 2
-1
Explanation
In this 3×3 grid, the starting cell (0, 0) contains a 1, which means it is blocked and cannot be used to begin the path. Since the path must start at (0, 0) and only move through cells with value 0, there is no valid path to reach the bottom-right cell (2, 2). Therefore, the output is -1, indicating that no path exists.