Question
Number of Shortest Paths
You are given a city with n intersections (numbered 0 to n - 1) connected by bidirectional roads. The city is fully connected, and there is at most one road between any two intersections.
You are also given a 2D array roads, where roads[i] = [u, v, time] represents a road between intersections u and v that takes time minutes to travel.
Your task is to compute the number of different ways to travel from intersection 0 to intersection n - 1 in the shortest possible time.
Input
- The first line contains an integer
n— the number of intersections. - The second line contains an integer
m— the number of roads. - The next
mlines each contain 3 space-separated integers — the values of the 2D arrayroads.
Output
Print the number of ways you can arrive at your destination in the shortest amount of time. Since the answer may be large, return it modulo 109 + 7.
Example
Sample Input:
7
10
0 6 7
0 1 2
1 2 3
1 3 3
6 3 3
3 5 1
6 5 1
2 5 1
0 4 5
4 6 2
Sample Output:
4
Explanation
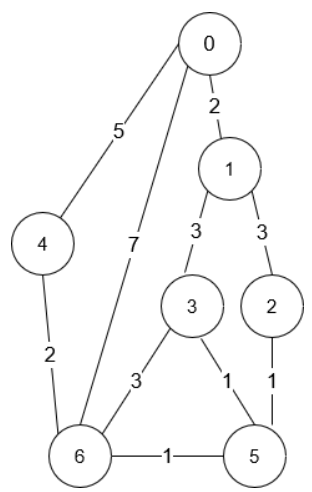
The shortest amount of time it takes to go from intersection 0 to intersection 6 is 7 minutes.
The four ways to get there in 7 minutes are:
- 0 ➝ 6
- 0 ➝ 4 ➝ 6
- 0 ➝ 1 ➝ 2 ➝ 5 ➝ 6
- 0 ➝ 1 ➝ 3 ➝ 5 ➝ 6
7
10
0 6 7
0 1 2
1 2 3
1 3 3
6 3 3
3 5 1
6 5 1
2 5 1
0 4 5
4 6 2
Sample Output:
4
Explanation

The shortest amount of time it takes to go from intersection 0 to intersection 6 is 7 minutes.
The four ways to get there in 7 minutes are:
- 0 ➝ 6
- 0 ➝ 4 ➝ 6
- 0 ➝ 1 ➝ 2 ➝ 5 ➝ 6
- 0 ➝ 1 ➝ 3 ➝ 5 ➝ 6