Question
All points collection
You are given an array points representing the integer coordinates of several points on a 2D plane, where each element is of the form: points[i] = [xi, yi].
The cost of connecting two points [xi, yi] and [xj, yj] is defined as their manhattan distance: |xi - xj| + |yi - yj|
Here |val| denotes the absolute value of val.
Print the minimum cost required to connect all the points. The points are considered connected if there is exactly one simple path between any two points.
Input
First line consists of one integer n number of coordinates.
Next n lines each contain two spaced integers representing points.
Next n lines each contain two spaced integers representing points.
Output
Print the minimum cost to make all points connected.
Example
Sample Input
5
0 0
2 2
3 10
5 2
7 0
Sample Output
20
Explanation
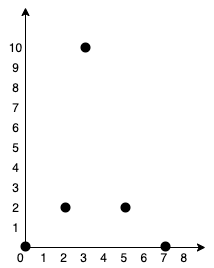
5
0 0
2 2
3 10
5 2
7 0
Sample Output
20
Explanation

The points can be connected in this way in minimum cost:
- (0, 0) → (2, 2): cost = 4
- (2, 2) → (3, 10): cost = 9
- (2, 2) → (5, 2): cost = 3
- (5, 2) → (7, 0): cost = 4
Total Cost: 4 + 9 + 3 + 4 = 20
This forms a Minimum Spanning Tree with exactly one simple path between any two points.