Question
Path Sum Maximum
You are given a 2D matrix grid of size KaTeX can only parse string typed expression containing integer elements. You start at the top-left cell KaTeX can only parse string typed expression and want to reach the bottom-right cell KaTeX can only parse string typed expression.
If you are currently standing at cell KaTeX can only parse string typed expression, you can move in three directions:
-
Down (D) — move down to the cell KaTeX can only parse string typed expression
-
Right (R) — move right to the cell KaTeX can only parse string typed expression
-
Right-Down (RD) — move diagonally right-down to the cell KaTeX can only parse string typed expression
Your task is to find the maximum path sum along any path from KaTeX can only parse string typed expression to KaTeX can only parse string typed expression.
Input
The first line contains two integers KaTeX can only parse string typed expression and KaTeX can only parse string typed expression — the number of rows and columns in the grid.
Each of the next KaTeX can only parse string typed expression lines contains KaTeX can only parse string typed expression integers — the elements of the grid.
Each of the next KaTeX can only parse string typed expression lines contains KaTeX can only parse string typed expression integers — the elements of the grid.
Output
Print a single integer — the maximum path sum achievable going from KaTeX can only parse string typed expression to KaTeX can only parse string typed expression following the allowed movements.
Example
Input
3 3
-1 -2 3
-2 5 6
7 8 9
Output
21
Explanation
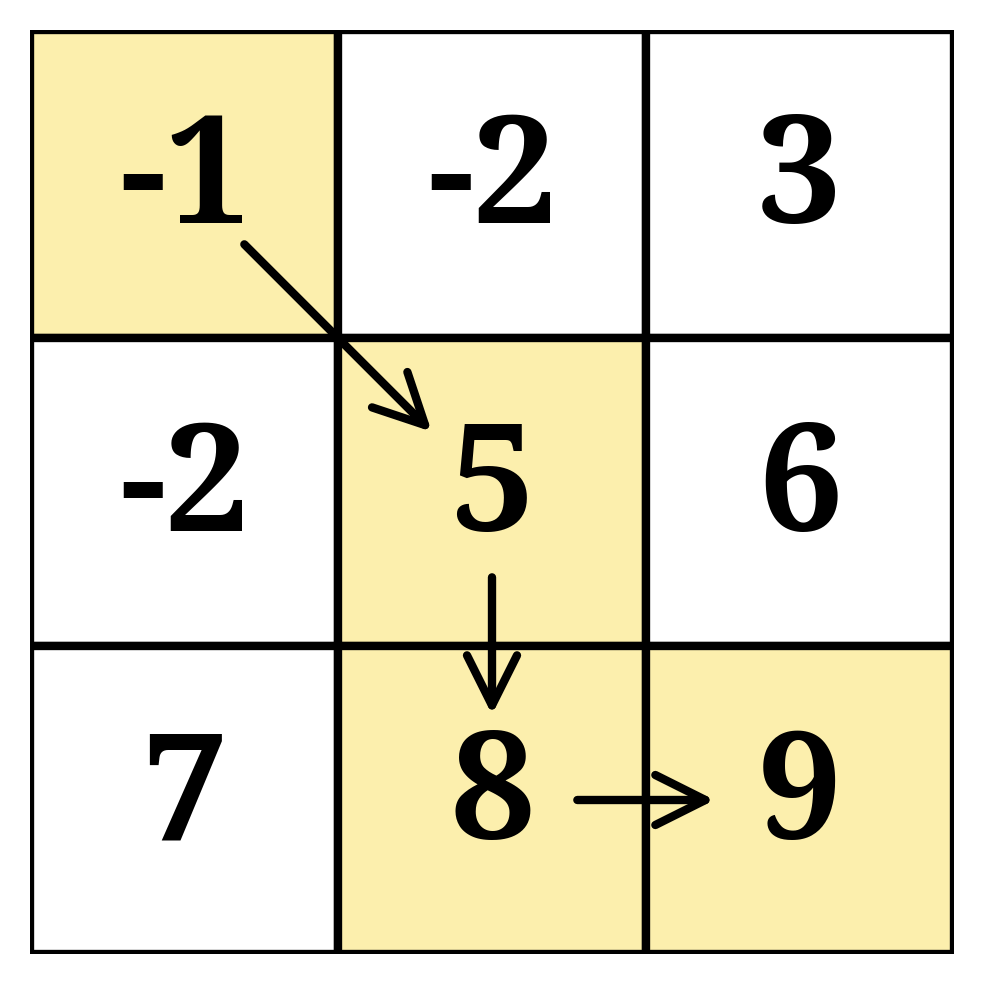 The path giving the maximum sum:
The path giving the maximum sum:
(0,0) → (1,1) → (2,1) → (2,2)
Sum = -1 + 5 + 8 + 9 = 21
This is the maximum path sum achievable going from (0,0) to (2,2) following the allowed movements.
Input
3 3
-1 -2 3
-2 10 6
17 8 3
Output
25
Explanation
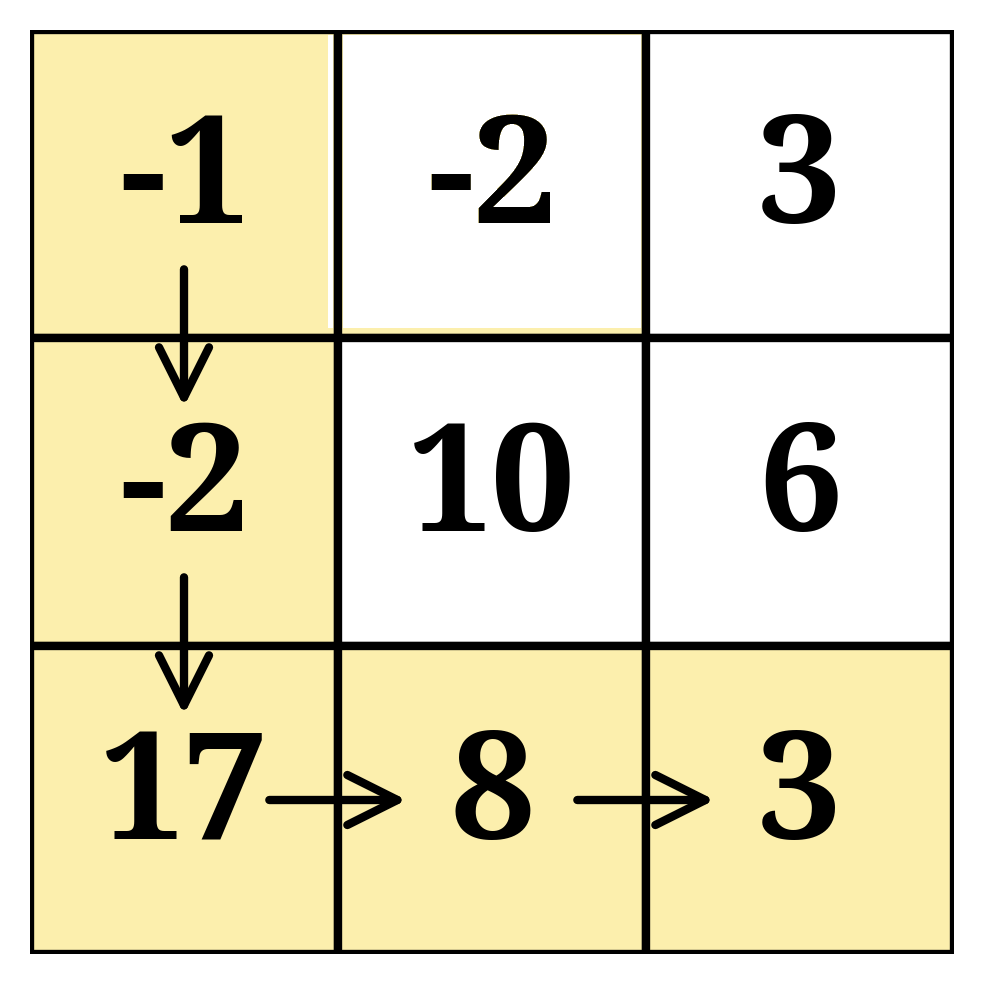
The path giving the maximum sum:
(0,0) → (1,0) → (2,0) → (2, 1) → (2, 2)
Sum = -1 + (-2) + 17 + 8 + 3 = 25
This is the maximum path sum achievable going from (0,0) to (2,2) following the allowed movements.
3 3
-1 -2 3
-2 5 6
7 8 9
Output
21
Explanation
 The path giving the maximum sum:
The path giving the maximum sum:
(0,0) → (1,1) → (2,1) → (2,2)
Sum = -1 + 5 + 8 + 9 = 21
This is the maximum path sum achievable going from (0,0) to (2,2) following the allowed movements.
Input
3 3
-1 -2 3
-2 10 6
17 8 3
Output
25
Explanation

The path giving the maximum sum:
(0,0) → (1,0) → (2,0) → (2, 1) → (2, 2)
Sum = -1 + (-2) + 17 + 8 + 3 = 25
This is the maximum path sum achievable going from (0,0) to (2,2) following the allowed movements.